|
|
|
Photons and the Photoelectric
Effect | |
|
 |
CONCEPTS AT A GLANCE The total energy
E and the linear momentum
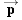
are
fundamental concepts in physics. We have seen in Chapters 6 and 7 how they apply
to moving particles, such as electrons and protons. The total energy of a
(nonrelativistic) particle is the sum of its kinetic energy (KE) and potential
energy (PE), or
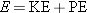
. The
magnitude
p of the particle’s momentum
is the product of its mass
m and speed
v, or
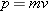
. These
particle concepts are listed in the upper-right portion of the
Concepts-at-a-Glance chart in Figure 29-3. We will now discuss the fact that
electromagnetic waves are composed of particle-like entities called
photons, and the
lower-right portion of the chart shows that the ideas of energy and momentum
also apply to them. However, as we will see, the equations defining photon
energy (
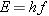
) and
momentum (
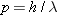
) are
different from those for a particle, as the chart indicates.
 |
 |
|
|
 |
Figure 29-3 CONCEPTS AT A GLANCE A moving
particle has energy E
and momentum p. An
electromagnetic wave is composed of particle-like entities
called photons, each of which also has energy and momentum.
Although the spotlight beams in the photograph look like
continuous beams of light, each is composed of discrete
photons. (Cameron Spencer/Getty Images News and Sport
Services)
| |
 | |
 |
Experimental evidence that light consists of photons comes from a
phenomenon called the
photoelectric effect, in
which electrons are emitted from a metal surface when light shines on it. Figure
29-4 illustrates the effect. The electrons are emitted if the light being used
has a sufficiently high frequency. The ejected electrons move toward a positive
electrode called the
collector and cause
a current to register on the ammeter. Because the electrons are ejected with the
aid of light, they are called
photoelectrons. As will be
discussed shortly, a number of features of the photoelectric effect could not be
explained solely with the ideas of classical physics.
 |
 |
|
|
 |
Figure 29-4 In
the photoelectric effect, light with a sufficiently high
frequency ejects electrons from a metal surface. These
photoelectrons, as they are called, are drawn to the positive
collector, thus producing a
current.
| |
 | |
 |
In 1905 Einstein presented an explanation of the photoelectric effect that
took advantage of Planck’s work concerning blackbody radiation. It was primarily
for his theory of the photoelectric effect that he was awarded the Nobel Prize
in physics in 1921. In his photoelectric theory, Einstein proposed that light of
frequency
f could be regarded as a
collection of discrete packets of energy (photons), each packet containing an
amount of energy
E given by
where
h is Planck’s constant. The light energy given
off by a light bulb, for instance, is carried by photons. The brighter the bulb,
the greater is the number of photons emitted per second. Example 1 estimates the
number of photons emitted per second by a typical light bulb.

|
Example 1 |
| |
Photons from a Light
Bulb | |
In converting electrical energy into light energy, a sixty-watt
incandescent light bulb operates at about 2.1% efficiency. Assuming that
all the light is green light ( 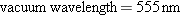 ),
determine the number of photons per second given off by the
bulb.
Reasoning The number of
photons emitted per second can be found by dividing the amount of light
energy emitted per second by the energy E of one photon. The energy of a single
photon is 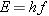 ,
according to Equation 29.2. The frequency f of the photon is related to its
wavelength 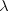 by
Equation 16.1 as 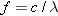 .
Solution At an efficiency
of 2.1%, the light energy emitted per second by a sixty-watt bulb is 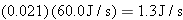 . The
energy of a single photon is
Therefore,
|
 |
Need more practice?
 |
 |
| Interactive LearningWare29.1 |
|
Example 1 calculates the number of photons per second given off
by a sixty-watt incandescent light bulb. The photons are em itted
uniformly in all directions. From a distance of 3.1 m you
glance at this bulb for 0.10 s. The light from the bulb travels
directly to your eye and does not reflect from anything. The pupil
of the eye has a diameter of 2.0 mm.How many photons enter your
eye?
Related
Homework: Problem
9
| |
According to Einstein, when light shines on a metal, a photon can give up
its energy to an electron in the metal. If the photon has enough energy to do
the work of removing the electron from the metal, the electron can be ejected.
The work required depends on how strongly the electron is held. For the
least strongly held electrons, the necessary
work has a minimum value
W0
and is called the
work
function of the metal. If a photon has energy in excess of the work
needed to remove an electron, the excess appears as kinetic energy of the
ejected electron. Thus, the least strongly held electrons are ejected with the
maximum kinetic energy KE
max. Einstein applied the
conservation-of-energy principle and proposed the following relation to describe
the photoelectric effect:
According to this equation,
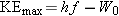
, which is
plotted in Figure 29-5, with KE
max along the
y axis and
f along the
x axis. The graph is a straight line that
crosses the
x axis at
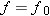
. At this
frequency, the electron departs from the metal with no kinetic energy (
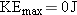
).
According to Equation 29.3, when
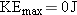
the energy
hf0 of the incident photon is
equal to the work function
W0
of the metal:
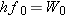
.
 |
 |
|
|
 |
Figure 29-5 Photons
can eject electrons from a metal when the light frequency is
above a minimum value f0. For
frequencies above this value, ejected electrons have a maximum
kinetic energy KEmax that is linearly related to
the frequency, as the graph
shows.
| |
 | |
 |
The photon concept provides an explanation for a number of features of the
photoelectric experiment that are difficult to explain without photons. It is
observed, for instance, that only light with a frequency above a certain minimum
value f0 will eject
electrons. If the frequency is below this value, no electrons are ejected,
regardless of how intense the light is. Example 2 determines the minimum
frequency value for a silver surface.

|
Example 2 |
| |
The Photoelectric Effect for
a Silver Surface | |
The work function for a silver surface is 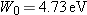 .
Find the minimum frequency that light must have to eject electrons from
this surface.
Reasoning The minimum
frequency f0 is that
frequency at which the photon energy equals the work function W0 of the metal, so the
electron is ejected with zero kinetic energy. Since 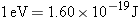 , the
work function expressed in joules is
Using Equation 29.3, we find
Solution The minimum
frequency f0 is
Photons with frequencies less
than f0 do not have
enough energy to eject electrons from a silver surface. Since 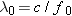 , the
wavelength of this light is 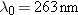 ,
which is in the ultraviolet region of the electromagnetic
spectrum. |
 |
In Example 2 the electrons are ejected with no kinetic energy, because the
light shining on the silver surface has the minimum possible frequency that will
eject them. When the frequency of the light exceeds this minimum value, the
electrons that are ejected do have kinetic energy. The next example deals with
such a situation.
|
Problem solving
insight The work function of a
metal is the minimum energy needed to eject an electron from the metal. An
electron that has received this minimum energy has no kinetic energy once
outside the metal. |
|
A N A L Y Z I N G
M U L T I P L E - C O N C E P T
P R O B L E M S |

|
Example 3 |
| |
The Maximum Speed of
Ejected Photoelectrons | |
|
Light with a wavelength of 95 nm shines on a selenium
surface, which has a work function of 5.9 eV. The ejected
electrons have some kinetic energy. Determine the maximum speed with
which electrons are ejected.
Reasoning The
maximum speed of the ejected electrons is related to their maximum
kinetic energy. Conservation of energy dictates that this maximum
kinetic energy is related to the work function of the surface and
the energy of the incident photons. The work function is given. The
energy of the photons can be obtained from the frequency of the
light, which is related to the wavelength.
Knowns and Unknowns
We have the following data:
|
Description |
Symbol |
Value |
Comment |
|
Wavelength of light |
|
95 nm |
|
|
Work function of selenium surface |
W0 |
5.9 eV |
Will be converted to joules |
|
Unknown
Variable |
|
|
|
|
Maximum speed of photoelectrons |
vmax |
? |
| |
|
 |
Modeling the
Problem
|
Step 1 Kinetic Energy and Speed |
|
The maximum kinetic energy KE max of the ejected
electrons is 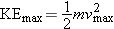
where m is the mass of an
electron. Solving for the maximum speed vmax gives Equation 1
at the right. The mass of the electron is 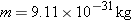
(see inside of front cover). The maximum kinetic energy is unknown,
but we will evaluate it in Step 2.
|
|
Step 2 Conservation of Energy |
|
According to the principle of conservation of energy, as
expressed by Equation 29.2, we have
where f is the frequency of the light.
Solving for KE max gives
which can be substituted
into Equation 1 as shown at the right. In this expression the work
function W0 is
known, and we will deal with the unknown frequency f in Step 3.
|
|
Step 3 Relationship between Frequency and
Wavelength |
|
The frequency and wavelength of the light are related to the
speed of light c according
to 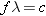
(Equation 16.6). Solving for the frequency gives
which we substitute into
Equation (2), as shown at the right.
|
Solution Combining the
results of each step algebraically, we find that
Thus, the maximum speed of the
photoelectrons is
Note in this calculation that
we have converted the value of the work function from electron volts to
joules.
Related Homework: Problem 8, 44 |
Another significant feature of the photoelectric effect is that the maximum
kinetic energy of the ejected electrons remains the same when the intensity of
the light increases, provided the light frequency remains the same. As the light
intensity increases, more photons per second strike the metal, and consequently
more electrons per second are ejected. However, since the frequency is the same
for each photon, the energy of each photon is also the same. Thus, the ejected
electrons always have the same maximum kinetic energy.
Whereas the photon model of light explains the photoelectric effect
satisfactorily, the electromagnetic wave model of light does not. Certainly, it
is possible to imagine that the electric field of an electromagnetic wave would
cause electrons in the metal to oscillate and tear free from the surface when
the amplitude of oscillation becomes large enough. However, were this the case,
higher-intensity light would eject electrons with a greater maximum kinetic
energy, a fact that experiment does not confirm. Moreover, in the
electromagnetic wave model, a relatively long time would be required with
low-intensity light before the electrons would build up a sufficiently large
oscillation amplitude to tear free. Instead, experiment shows that even the
weakest light intensity causes electrons to be ejected almost instantaneously,
provided the frequency of the light is above the minimum value f0. The failure of the
electromagnetic wave model to explain the photoelectric effect does not mean
that the wave model should be abandoned. However, we must recognize that the
wave model does not account for all the characteristics of light. The photon
model also makes an important contribution to our understanding of the way light
behaves when it interacts with matter.
 Check Your Understanding
1 Check Your Understanding
1 |
|
In the photoelectric effect, electrons are ejected from the surface
of a metal when light shines on it. Which one or more of the following
would lead to an increase in the maximum kinetic energy of the ejected
electrons? (a) Increasing the frequency of the incident light, (b)
Increasing the number of photons per second striking the surface. (c)
Using photons whose frequency f0 is less than W0/h, where W0 is the work function of
the metal and h is Planck’s constant. (d) Selecting a metal that has a
greater work function. (The answer is
given at the end of the book.)
Background: The
conservation of energy relates the maximum kinetic energy of the ejected
electrons to the energy of the incident photons and the work function of
the metal. This relation, Equation 29.3, holds the key to understanding
the photoelectric effect.
For similar
questions (including calculational counterparts), consult Self-Assessment
Test 29.1, which is described at the
end of this section. |
Because a photon has energy, the photon can eject an electron from a metal
surface when it interacts with the electron. However, a photon is different from
a normal particle. A normal particle has a mass and can travel at speeds up to,
but not equal to, the speed of light. A photon, on the other hand, travels at
the speed of light in a vacuum and does not exist as an object at rest. The
energy of a photon is entirely kinetic in nature, because it has no rest energy
and no mass. To show that a photon has no mass, we rewrite Equation 28.4 for the
total energy
E as
The term
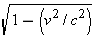
is zero
because a photon travels at the speed of light,
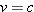
. Since the
energy
E of the photon is finite, the
left side of the equation above is zero. Thus, the right side must also be zero,
so
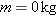
and the
photon has no mass.
|
The physics of
charge-coupled devices and digital
cameras. |
One of the most exciting and useful applications of the photoelectric
effect is the charge-coupled device (CCD). An array of these devices is used
instead of film in digital cameras (see Figure 29-6) to capture images in the
form of many small groups of electrons. CCD arrays are also used in digital
camcorders and electronic scanners, and they provide the method of choice with
which astronomers capture those spectacular images of the planets and the stars.
For use with visible light, a CCD array consists of a sandwich of semiconducting
silicon, insulating silicon dioxide, and a number of electrodes, as Figure 29-7
shows. The array is divided into many small sections, or pixels, sixteen of
which are shown in the drawing. Each pixel captures a small part of a picture.
Digital cameras can have up to eight million pixels, depending on price. The
greater the number of pixels, the better is the resolution of the photograph.
The blow-up in Figure 29-7 shows a single pixel. Incident photons of visible
light strike the silicon and generate electrons via the photoelectric effect.
The range of energies of the visible photons is such that approximately one
electron is released when a photon interacts with a silicon atom. The electrons
do not escape from the silicon, but are trapped within a pixel because of a
positive voltage applied to the electrodes beneath the insulating layer. Thus,
the number of electrons that are released and trapped is proportional to the
number of photons striking the pixel. In this fashion, each pixel in the CCD
array accumulates an accurate representation of the light intensity at that
point on the image. Color information is provided using red, green, or blue
filters or a system of prisms to separate the colors. Astronomers use CCD arrays
not only in the visible region of the electromagnetic spectrum but in other
regions as well.
 |
 |
|
|
 |
Figure 29-6 (a) Digital cameras like this
one use an array of charge-coupled devices instead of film to
capture an image. (YOSHIKAZU TSUNO/AFP/Getty Images) (b) Images taken by a digital
camera can be easily downloaded to a computer and sent to your
friends via the Internet. (Ross Woodhall/Taxi/Getty
Images)
| |
 | |
 |
 |
 |
|
|
 |
Figure 29-7 A
CCD array can be used to capture photographic images using the
photoelectric effect.
| |
 | |
 |
In addition to trapping the photoelectrons, the electrodes beneath the
pixels are used to read out the electron representation of the picture. By
changing the positive voltages applied to the electrodes, it is possible to
cause all of the electrons trapped in one row of pixels to be transferred to the
adjacent row. In this fashion, for instance, row 1 in Figure 29-7 is transferred
into row 2, row 2 into row 3, and row 3 into the bottom row, which serves a
special purpose. The bottom row functions as a horizontal shift register, from
which the contents of each pixel can be shifted to the right, one at a time, and
read into an analog signal processor. This processor senses the varying number
of electrons in each pixel in the shift register as a kind of wave that has a
fluctuating amplitude. After another shift in rows, the information in the next
row is read out, and so forth. The output of the analog signal processor is sent
to an analog-to-digital converter, which produces a digital representation of
the image in terms of the zeros and ones that computers recognize.
Look back at the spectacular photograph at the beginning of this chapter.
It shows the central portion of the Eagle Nebula, a giant star-forming region
some 7000 light-years from earth. The photo was taken by the Hubble Space
Telescope and reveals towering clouds of molecular gas and dust, in which there
is dramatic evidence of the energy carried by photons. These clouds extend more
than a light-year from base to tip and are the birthplace of stars. A star
begins to form within a cloud when the gravitational force pulls together
sufficient gas to create a high-density “ball.” When the gaseous ball becomes
sufficiently dense, thermonuclear fusion (see Section 32.5) occurs at its core,
and the star begins to shine. The newly born stars are buried within the cloud
and cannot be seen from earth. However, the process of photoevaporation allows
astronomers to see many of the high-density regions where stars are being
formed. Photoevaporation is the process in which high-energy, ultraviolet (UV)
photons from hot stars outside the cloud heat it up, much like microwave photons
heat food in a microwave oven. Figure 29-9
a is a reproduction of the upper left portion
of the chapter-opening photo and shows streamers of gas photoevaporating from
the cloud as it is illuminated by stars located beyond the photograph’s upper
edge. As photoevaporation proceeds, globules of gas that are denser than their
surroundings are exposed. The globules are known as
evaporating gaseous globules (EGGs), and they
are slightly larger than our solar system. The drawing in part
b of Figure 29-9 shows that the EGGs shade the
gas and dust behind them from the UV photons, creating the many finger-like
protrusions seen on the surface of the cloud. Astronomers believe that some of
these EGGs contain young stars within them. In some cases, so much gas has
boiled off that a newborn star can be seen on the surface of an EGG (see the
circled feature in the chapter-opening photograph).
 |
 |
|
|
 |
Figure 29-9 (a) This is the upper left
portion of the chapter-opening photograph. Photoevaporation
produces finger-like projections on the surface of the gas
clouds in the Eagle Nebula. At the fingertips are high-density
evaporating gaseous globules (EGGs). (Courtesy NASA) (b) This drawing illustrates
the photoevaporation that is occurring in the photograph in
part (a).
| |
 | |
 |
|
The physics of
photoevaporation and star
formation. |

|
Test your understanding of the material in Sections 29.1, 29.2 and
29.3 :
 |
|
· |
The Wave-Particle Duality |
 |
|
· |
Blackbody Radiation and Planck’s Constant |
 |
|
· |
Photons |
 |
|
· |
The Photoelectric Effect |
 | |
|
 |
| Copyright © 2007 John Wiley & Sons,
Inc. All rights reserved. |
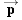 are
fundamental concepts in physics. We have seen in Chapters 6 and 7 how they apply
to moving particles, such as electrons and protons. The total energy of a
(nonrelativistic) particle is the sum of its kinetic energy (KE) and potential
energy (PE), or
are
fundamental concepts in physics. We have seen in Chapters 6 and 7 how they apply
to moving particles, such as electrons and protons. The total energy of a
(nonrelativistic) particle is the sum of its kinetic energy (KE) and potential
energy (PE), or 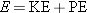 . The
magnitude p of the particle’s momentum
is the product of its mass m and speed
v, or
. The
magnitude p of the particle’s momentum
is the product of its mass m and speed
v, or 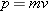 . These
particle concepts are listed in the upper-right portion of the
Concepts-at-a-Glance chart in Figure 29-3. We will now discuss the fact that
electromagnetic waves are composed of particle-like entities called photons, and the
lower-right portion of the chart shows that the ideas of energy and momentum
also apply to them. However, as we will see, the equations defining photon
energy (
. These
particle concepts are listed in the upper-right portion of the
Concepts-at-a-Glance chart in Figure 29-3. We will now discuss the fact that
electromagnetic waves are composed of particle-like entities called photons, and the
lower-right portion of the chart shows that the ideas of energy and momentum
also apply to them. However, as we will see, the equations defining photon
energy (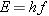 ) and
momentum (
) and
momentum (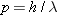 ) are
different from those for a particle, as the chart indicates.
) are
different from those for a particle, as the chart indicates.
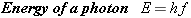
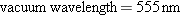 ),
determine the number of photons per second given off by the
bulb.
),
determine the number of photons per second given off by the
bulb.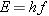 ,
according to Equation 29.2. The frequency f of the photon is related to its
wavelength
,
according to Equation 29.2. The frequency f of the photon is related to its
wavelength 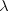 by
Equation 16.1 as
by
Equation 16.1 as 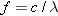 .
.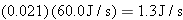 . The
energy of a single photon is
. The
energy of a single photon is


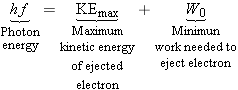
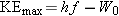 , which is
plotted in Figure 29-5, with KEmax along the y axis and f along the x axis. The graph is a straight line that
crosses the x axis at
, which is
plotted in Figure 29-5, with KEmax along the y axis and f along the x axis. The graph is a straight line that
crosses the x axis at 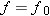 . At this
frequency, the electron departs from the metal with no kinetic energy (
. At this
frequency, the electron departs from the metal with no kinetic energy (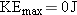 ).
According to Equation 29.3, when
).
According to Equation 29.3, when 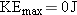 the energy
hf0 of the incident photon is
equal to the work function W0
of the metal:
the energy
hf0 of the incident photon is
equal to the work function W0
of the metal: 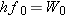 .
.
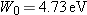 .
Find the minimum frequency that light must have to eject electrons from
this surface.
.
Find the minimum frequency that light must have to eject electrons from
this surface.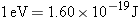 , the
work function expressed in joules is
, the
work function expressed in joules is
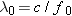 , the
wavelength of this light is
, the
wavelength of this light is 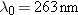 ,
which is in the ultraviolet region of the electromagnetic
spectrum.
,
which is in the ultraviolet region of the electromagnetic
spectrum.
 Check Your Understanding
1
Check Your Understanding
1
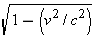 is zero
because a photon travels at the speed of light,
is zero
because a photon travels at the speed of light, 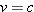 . Since the
energy E of the photon is finite, the
left side of the equation above is zero. Thus, the right side must also be zero,
so
. Since the
energy E of the photon is finite, the
left side of the equation above is zero. Thus, the right side must also be zero,
so 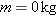 and the
photon has no mass.
and the
photon has no mass.