|
|
|
The Mass Defect of the Nucleus and Nuclear
Binding Energy | |
|
 |
Two ideas that we have studied previously come into play as we discuss the
binding energy of a nucleus. These are the rest energy of an object (Section
28.6) and mass (Section 4.2). In Einstein’s theory of special relativity, energy
and mass are equivalent; in fact, the rest energy
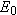
and the mass
m are related via
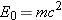
(Equation 28.5), where
c is the speed of light in a vacuum.
Therefore, a change
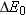
in the rest energy of the system is equivalent to a
change
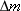
in the
mass of the system, according to
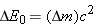
. We see, then, that the binding energy used in
Figure 31-3 to disassemble the nucleus appears as extra mass of the separated
and stationary nucleons. In other words, the sum of the individual masses of the
separated protons and neutrons is greater by an amount
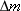
than the mass of the stable
nucleus. The difference in mass
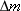
is known as the
mass defect of the
nucleus.
As Example 2 shows, the binding energy of a nucleus can be determined from
the mass defect according to Equation 31.3:
 |
Example 2 |
| |
The Binding Energy of the Helium
Nucleus | |
The most abundant isotope of helium has a 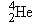 nucleus whose mass is 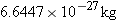 . For this
nucleus, find (a) the mass defect and (b) the binding energy.
Reasoning The symbol 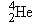 indicates
that the helium nucleus contains 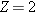 protons and 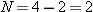 neutrons. To obtain the mass
defect 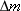 ,
we first determine the sum of the individual masses of the separated
protons and neutrons. Then we subtract from this sum the mass of the 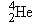 nucleus.
Finally, we use Equation 31.3 to calculate the binding energy from the
value for 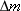 .
Solution
 |
|
a. |
Using data from Table 31-1, we find that the sum of the
individual masses of the nucleons is
This value is
greater than the mass of the intact 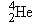 nucleus, and the
mass defect is
|
 |
|
b. |
According to Equation 31.3, the binding energy is
Usually, binding
energies are expressed in energy units of electron volts
instead of joules 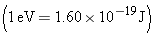 :
|
 | |
In this result, one million electron volts is denoted by the unit
MeV. The value of 28.3 MeV is more than two million times greater than the
energy required to remove an orbital electron from an atom. |
 |
In calculations such as that in Example 2, it is customary to use the
atomic mass unit (u)
instead of the kilogram. As introduced in Section 14.1, the atomic mass unit is
one-twelfth of the mass of a
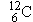
atom of carbon. In terms of this unit, the mass of
a
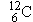
atom is
exactly 12 u. Table 31-1 also gives the masses of the electron, the proton, and
the neutron in atomic mass units. For future calculations, the energy equivalent
of one atomic mass unit can be determined by observing that the mass of a proton
is
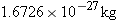
or 1.0073
u, so that
and
In electron volts, therefore, one atomic mass
unit is equivalent to
Data tables for isotopes, such as that in Appendix F, give masses in atomic
mass units. Typically, however, the given masses are not nuclear masses. They
are
atomic masses—that is, the masses of
neutral atoms, including the mass of the orbital electrons. Example 3 deals
again with th
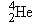
nucleus and shows how to take into account the effect of the orbital electrons
when using such data to determine binding energies.
 |
Example 3 |
| |
The Binding Energy of the Helium Nucleus,
Revisited | |
The atomic mass of 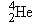 is 4.0026 u, and the atomic mass of 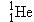 is 1.0078 u.
Using atomic mass units instead of kilograms, obtain the binding energy of
the 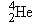
nucleus.
Solution The sum of the
individual masses is
The mass defect is 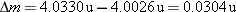 . Since 1 u is equivalent to
931.5 MeV, the binding energy is 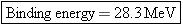 , which matches that obtained in Example
2. |
 |
 Check Your Understanding
2 Check Your Understanding
2 |
The following table gives values for the mass defect 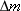 for four hypothetical
nuclei: A, B, C, and D. Which statement is true regarding the stability of
these nuclei? (a) Nucleus D is the most stable, and A is the least stable.
(b) Nucleus C is stable, whereas A, B, and D are not stable. (c) Nucleus A
is the most stable, and D is not stable. (d) Nuclei A and B are stable,
but B is more stable than A. (The answer
is given at the end of the book.)
| |
A |
B |
C |
D |
Mass defect, 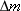 |
|
|
0 kg |
| |
Background: The mass
defect of a nucleus is the sum of the individual masses of the separated
nucleons minus the mass of the intact nucleus. The binding energy of a
nucleus is the energy required to separate it into its constituent protons
and neutrons. The greater the binding energy, the more stable is the
nucleus. The binding energy and the mass defect are related.
For similar
questions (including calculational counterparts), consult Self-Assessment
Test 31.1,
which is described at the end of Section
31.5. |
 |
| Copyright © 2007 John Wiley & Sons,
Inc. All rights reserved. |
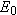 and the mass m are related via
and the mass m are related via 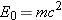 (Equation 28.5), where c is the speed of light in a vacuum.
Therefore, a change
(Equation 28.5), where c is the speed of light in a vacuum.
Therefore, a change 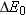 in the rest energy of the system is equivalent to a
change
in the rest energy of the system is equivalent to a
change 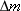 in the
mass of the system, according to
in the
mass of the system, according to 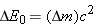 . We see, then, that the binding energy used in
Figure 31-3 to disassemble the nucleus appears as extra mass of the separated
and stationary nucleons. In other words, the sum of the individual masses of the
separated protons and neutrons is greater by an amount
. We see, then, that the binding energy used in
Figure 31-3 to disassemble the nucleus appears as extra mass of the separated
and stationary nucleons. In other words, the sum of the individual masses of the
separated protons and neutrons is greater by an amount 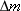 than the mass of the stable
nucleus. The difference in mass
than the mass of the stable
nucleus. The difference in mass 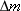 is known as the mass defect of the
nucleus.
is known as the mass defect of the
nucleus.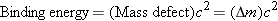
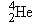 nucleus whose mass is
nucleus whose mass is 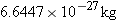 . For this
nucleus, find (a) the mass defect and (b) the binding energy.
. For this
nucleus, find (a) the mass defect and (b) the binding energy.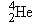 indicates
that the helium nucleus contains
indicates
that the helium nucleus contains 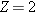 protons and
protons and 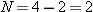 neutrons. To obtain the mass
defect
neutrons. To obtain the mass
defect 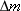 ,
we first determine the sum of the individual masses of the separated
protons and neutrons. Then we subtract from this sum the mass of the
,
we first determine the sum of the individual masses of the separated
protons and neutrons. Then we subtract from this sum the mass of the 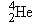 nucleus.
Finally, we use Equation 31.3 to calculate the binding energy from the
value for
nucleus.
Finally, we use Equation 31.3 to calculate the binding energy from the
value for 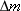 .
.
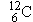 atom of carbon. In terms of this unit, the mass of
a
atom of carbon. In terms of this unit, the mass of
a 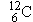 atom is
exactly 12 u. Table 31-1 also gives the masses of the electron, the proton, and
the neutron in atomic mass units. For future calculations, the energy equivalent
of one atomic mass unit can be determined by observing that the mass of a proton
is
atom is
exactly 12 u. Table 31-1 also gives the masses of the electron, the proton, and
the neutron in atomic mass units. For future calculations, the energy equivalent
of one atomic mass unit can be determined by observing that the mass of a proton
is 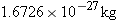 or 1.0073
u, so that
or 1.0073
u, so that
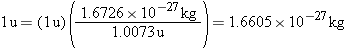
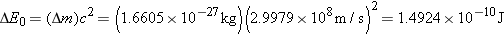
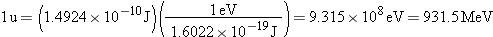
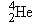 nucleus and shows how to take into account the effect of the orbital electrons
when using such data to determine binding energies.
nucleus and shows how to take into account the effect of the orbital electrons
when using such data to determine binding energies.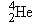 is 4.0026 u, and the atomic mass of
is 4.0026 u, and the atomic mass of 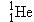 is 1.0078 u.
Using atomic mass units instead of kilograms, obtain the binding energy of
the
is 1.0078 u.
Using atomic mass units instead of kilograms, obtain the binding energy of
the 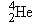 nucleus.
nucleus.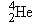 includes the
mass of the two electrons in the neutral helium atom. To calculate
the mass defect, we must subtract 4.0026 u from the sum of the individual
masses of the nucleons, including the mass of the electrons. As Figure
31-4 illustrates, the electron mass will be included if the masses of two
hydrogen atoms are used in the calculation instead of the masses of two
protons. The mass of a
includes the
mass of the two electrons in the neutral helium atom. To calculate
the mass defect, we must subtract 4.0026 u from the sum of the individual
masses of the nucleons, including the mass of the electrons. As Figure
31-4 illustrates, the electron mass will be included if the masses of two
hydrogen atoms are used in the calculation instead of the masses of two
protons. The mass of a 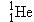 hydrogen atom is given in Table 31-1 as
1.0078 u, and the mass of a neutron as 1.0087 u.
hydrogen atom is given in Table 31-1 as
1.0078 u, and the mass of a neutron as 1.0087 u.
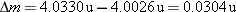 . Since 1 u is equivalent to
931.5 MeV, the binding energy is
. Since 1 u is equivalent to
931.5 MeV, the binding energy is 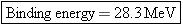 , which matches that obtained in Example
2.
, which matches that obtained in Example
2.
 isotope of helium indicates that
the
isotope of helium indicates that
the  nucleus is
particularly stable. The binding energy per nucleon increases rapidly for nuclei
with small masses and reaches a maximum of approximately 8.7 MeV/nucleon for a
nucleon number of about
nucleus is
particularly stable. The binding energy per nucleon increases rapidly for nuclei
with small masses and reaches a maximum of approximately 8.7 MeV/nucleon for a
nucleon number of about 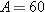 . For greater nucleon numbers, the binding energy
per nucleon decreases gradually. Eventually, the binding energy per nucleon
decreases enough so there is insufficient binding energy to hold the nucleus
together. Nuclei more massive than the
. For greater nucleon numbers, the binding energy
per nucleon decreases gradually. Eventually, the binding energy per nucleon
decreases enough so there is insufficient binding energy to hold the nucleus
together. Nuclei more massive than the 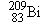 nucleus of bismuth are unstable and hence
radioactive.
nucleus of bismuth are unstable and hence
radioactive.
 Check Your Understanding
2
Check Your Understanding
2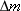 for four hypothetical
nuclei: A, B, C, and D. Which statement is true regarding the stability of
these nuclei? (a) Nucleus D is the most stable, and A is the least stable.
(b) Nucleus C is stable, whereas A, B, and D are not stable. (c) Nucleus A
is the most stable, and D is not stable. (d) Nuclei A and B are stable,
but B is more stable than A. (The answer
is given at the end of the book.)
for four hypothetical
nuclei: A, B, C, and D. Which statement is true regarding the stability of
these nuclei? (a) Nucleus D is the most stable, and A is the least stable.
(b) Nucleus C is stable, whereas A, B, and D are not stable. (c) Nucleus A
is the most stable, and D is not stable. (d) Nuclei A and B are stable,
but B is more stable than A. (The answer
is given at the end of the book.)